- Perceptron (퍼셉트론)
퍼셉트론은 딥러닝에서 사용된다. 이것은 인간의 뉴런을 본 떠 만들었다. 퍼셉트론은 다수의 신호(Input)를 입력받아서 하나의 신호(Output)를 출력한다. 이는 뉴런이 전기신호를 내보내 정보를 전달하는 것과 비슷하게 동작한다. 퍼셉트론의 Weight(가중치)는 뉴런끼리 서로의 신호를 전달하는 것과 같은 역할을 한다.

Weight(가중치)는 각각의 입력신호에 부여되어 입력신호와의 계산을 하고 신호의 총합이 정해진 임계값(θ; theta,세타)을 넘었을 때 1을 출력한다. (이를 뉴련의 활성화activation 으로도 표현) 넘지 못하면 0 또는 -1을 출력한다. 결론적으로 우리는 딥러닝을 통해 Weight(가중치)의 값을 조정함으로서 원하는 모델을 만들어내고자 한다.
편향(Bias)은 학습 데이터가 가중치와 계산되어 넘어야 하는 임계점으로, 이 값이 높으면 높을수록 분류의 기준이 엄격하고 낮을수록 한계점이 낮아져 데이터의 허용 범위가 넓어진다.

Bias가 높을수록
모델이 간단해지는 경향이 있고 (변수가 적고 일반화됨)
과소적합(Underfitting : 모델이 너무 단순해서 데이터의 내재된 구조를 학습하지 못하는 현상)이 발생할 수 있다.
편향이 낮을수록
모델이 복잡해지고
오버피팅(Overfitting)이 발생할 수 있으며
필요없는 노이즈가 포함될 가능성이 높아진다.
퍼셉트론은 AND, OR , NAND, XOR 게이트 등으로 구성되어있다. 디지털논리회로와 비슷하다. 입력값에 따라 원하는 출력값을 만들어내기 위해 이런 저런 단순한 게이트들을 이용하여 원하는 결과를 도출해낸다. 하지만 단층 퍼셉트론은 원하는 결과를 모두 도출해낼 수는 없다. 예를 들어, 0부터 9까지 차례대로 나타내는 프로그램을 만든다고 가정하면 딱 하나의 게이트로는 절대 이런 프로그램을 만들어낼 수 없다. 하지만 여러 개의 게이트를 사용할 수 있다면 가능할 것이다. 이렇게 단층 퍼셉트론으로 불가능한 것을 하기 위해 우리는 다층 퍼셉트론을 사용한다.
- 다층 퍼셉트론

퍼셉트론이 여러개의 층으로 이루어지는 것을 다층 퍼셉트론이라고 한다. Input은 입력층, Hidden은 은닉층, Output은 출력층으로 표현한다. 여기서 은닉층(Hidden)이 여러개를 갖게 되는 것을 다층 퍼셉트론이라고 할 수 있다.
| model = Sequential() model.add(Dense(12, input_dim=8, activation='relu')) model.add(Dense(8, activation='relu')) model.add(Dense(1, activation='sigmoid')) |
위의 코드는 다층퍼셉트론을 만드는 기본적인 코드이다. 코드에서 activation에 있는 relu와 sigmoid는 활성화 함수이다.
- 활성화 함수

위의 그림은 신경망을 나타내는 그림이다. 여기서 활성화 함수에 해당하는 것은 계단함수이다.
- 계단함수
계단함수라는 것은 특정 임계값을 넘기면 활성화되는, 즉 0과 1로 출력되는 함수를 의미한다.
| import matplotlib.pylab as plt import numpy as np def step_function(x) : result = x > 0 return result.astype(np.int) x = np.arange(-5,5,0.1) y = step_function(x) plt.plot(x,y) plt.ylim(-0.1,1.1) plt.show() |

위와 같은 코드를 입력하면 파이썬으로 계단함수를 구현할 수 있다.
하지만 단층퍼셉트론이 아니라 다층퍼셉트론 같은 경우는 활성화 함수로 계단함수를 쓸 수 있을까? 어떤 기준으로 0과 1을 나눠야 하는걸까? 그것에 대한 해답이 sigmoid와 relu이다.
- sigmoid
| import matplotlib.pylab as plt import numpy as np def sigmoid(x) : return 1/(1+np.exp(-x)) x = np.array([-1,1,2]) sigmoid(x) x = np.arange(-5,5,0.1) y = sigmoid(x) plt.plot(x,y) plt.ylim(-0.1,1.1) plt.show() |

위와 같은 코드를 입력하면 파이썬으로 Sigmoid 함수를 구현할 수 있다.
Sigmoid 함수는 그래프 그대로 데이터를 0과 1로 분류한다. 퍼셉트론은 인간의 뉴런을 모델로 했기 때문에 다층 퍼셉트론같은 경우 데이터를 0과 1로 구분하여 역치 이상(1)일 경우 데이터를 다음 퍼셉트론으로 넘기는 방식으로 운영되어진다. 계단함수나 Sigmoid나 둘 다 0 또는 1 혹은 0~1 사이의 값으로 데이터를 변환해준다.
그런데 왜 단층퍼셉트론에는 계단함수를 쓰고 다층퍼셉트론에서는 Sigmoid 또는 ReLU를 사용하는 것일까?
다층 퍼셉트론은 여러개의 은닉층을 보유하고 앞에서 가공되어진 데이터들이 다음 은닉층으로 넘어가는 구조이다. 계단함수를 다층 퍼셉트론에서 사용한다면 우리는 이전 데이터를 오직 0과 1, 즉 극단적인 형태로밖에 받을 수 없고 이런식이라면 다층 퍼셉트론을 만들어 좋은 모델을 만들 수 없게 된다. 하지만 Sigmoid 함수같은 경우는 값을 0~1 사이로 만들어주기 때문에 가공된 데이터를 다음 은닉층으로 보내줘도 극단적인 형태가 아니고 신경망이 데이터를 섬세하게 분류할 수 있도록 도와준다.
그런데 ReLU는 또 왜 필요한걸까?
- ReLU
| import matplotlib.pylab as plt import numpy as np def relu(x) : return np.maximum(0,x) x = np.arange(-5,5,0.1) y = relu(x) plt.plot(x,y) plt.ylim(-0.5,5.5,0.1) plt.show() |
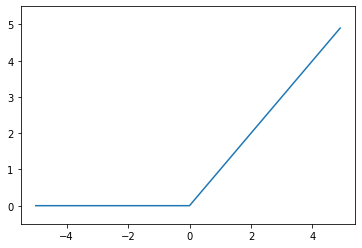
위와 같은 코드를 입력하면 파이썬으로 ReLU 함수를 구현할 수 있다.
ReLU함수는 Sigmoid의 단점을 해결하기 위해 나왔다. Sigmoid 함수의 단점은 0과 1사이의 데이터로 이루어져 있어 역전파를 할수록, 즉 층이 깊어질수록 활성화 값들이 0과 1에 치우쳐져 있어 미분값이 0에 가까워진다는 것이다.
이것을 Vanishing Gradient Problem(기울기 값이 사라지는 문제)이라고 한다. 즉, 전파가 역전파될 때 기울기 소실로 인해서 앞층까지 전파가 안된다는 이야기다. 따라서 이와 같은 문제점을 해결하고자 ReLU 함수를 사용하게 된 것이다.
ReLU는
0보다 작은 값에 대해서는 0을 반환하고,
0보다 큰 값에 대해서는 그 값을 그대로 반환하여
층이 깊어져도 0으로 수렴하는 오류를 범하지 않게 된다.
Leaky ReLU
| def leaky_relu(x) : return np.maximum(0.01*x,x) x = np.arange(-20,5,0.1) y = leaky_relu(x) plt.plot(x,y) plt.grid() plt.ylim(-0.5,5.5,0.1) plt.show() |

위와 같은 코드를 입력하면 파이썬으로 Leaky ReLU 함수를 구현할 수 있다.
ReLU와 동일하나 x가 음수일때 기울기(gradient)가 0.01이다.
ELU (Exponential Linear Units)

ELU 또한 ReLU와 비슷하나 기울기가 살아남는다는 특징이 있다.
'공부 > 인공지능' 카테고리의 다른 글
| 인공지능 정리9(배치(Batch), 미니배치 학습, 에폭(Epoch), SGD) (1) | 2023.12.10 |
|---|---|
| 인공지능 정리8(항등함수, Softmax함수) (0) | 2023.12.10 |
| 인공지능 정리6(Clustering(군집화)) (0) | 2023.12.10 |
| 인공지능 정리5(Classification(분류)) (0) | 2023.12.10 |
| 인공지능 정리4(회귀(Regression)) (0) | 2023.12.10 |